Área e perímetro no Enem: como o assunto é cobrado na prova

Cálculos de área e perímetro são constantes no Enem e um conteúdo necessário para quem quer garantir sua vaga no ensino superior.

Por isso, neste conteúdo, vamos falar sobre o que são a área e o perímetro, como esses dois conceitos se encaixam na geometria plana, quais são as fórmulas e como usá-las.

Além disso, ao final do conteúdo, também teremos alguns exercícios para você começar a praticar.

Você vai conferir:

• O que mais cai em matemática no Enem?
• A diferença entre área e perímetro
• O que é área e como calcular?
• O que é perímetro e como calcular?
• Exercícios de área e perímetro para você praticar
• Conclusão

O que mais cai em matemática no Enem?

O Enem, Exame Nacional do Ensino Médio, é uma prova que nasceu em 1998 para medir a qualidade do ensino médio brasileiro.

Hoje, porém, ela se tornou a principal forma de ingresso no ensino superior.

A prova do Enem reúne conteúdos presentes no currículo escolar do ensino médio divididos em quatro grandes áreas do conhecimento:

• Ciências Humanas e suas Tecnologias;
• Ciências da Natureza e suas Tecnologias;
• Linguagens, Códigos e suas Tecnologias;
• Matemática e suas Tecnologias.

Cada área conta com 45 questões objetivas, ou seja, o exame tem 180 perguntas no total.

Existe um documento elaborado pelo Ministério da Educação (o MEC), a Matriz de Referência do Enem, onde você pode conferir todas as matérias que caem na prova de Matemática e suas Tecnologias.

Diferente das outras provas, essa área do conhecimento não aborda mais do que uma disciplina. A prova de Matemática e suas Tecnologias foca na matemática.

Abaixo, fizemos um breve levantamento dos conteúdos que mais caem:

• Equações e funções de 1° e 2° grau;
• Porcentagem;
• Geometria plana e espacial;
• Regra de três;
• Matemática financeira;
• Razões e proporções;
• Noções de estatística;
• Circunferências;
• Leitura e interpretação de gráficos;

Dentre esses, geometria plana é um assunto recorrente na prova. Logo, entender como calcular área e perímetro pode ser essencial para tirar uma boa nota.

A diferença entre área e perímetro

Área e perímetro são conceitos que existem dentro da geometria plana, especificamente.

Ambos são utilizados para medir uma figura em duas dimensões, porém focam em aspectos diferentes. Por exemplo:

• Área: se refere à medida total que uma figura ocupa no plano;
• Perímetro: é a soma dos tamanhos dos segmentos de reta, ou seja, dos lados da figura.

O que é a geometria plana?

Também conhecida como euclidiana, a geometria plana é o estudo de figuras bidimensionais, em duas dimensões, aquelas que não têm volume.

Ela foi criada pelo matemático, Euclides de Alexandria, e explora as propriedades e os tamanhos de figuras planas aplicando fórmulas para encontrar sua área e perímetro.

A geometria plana utiliza alguns conceitos em seus estudos. São eles:

Conceitos Primitivos

• Ponto: a base de toda a geometria porque é a partir de um conjunto de pontos que se criam retas e, consequentemente, figuras no plano;
• Reta: são conjuntos de pontos entendidos como linhas sem curvas. As retas podem ser determinadas como objetos unidimensionais, que têm apenas uma dimensão;
• Plano: é um conjunto ilimitado e infinito de retas, superfície onde são encontradas figuras em duas dimensões. É dentro do plano que acontece a geometria plana;
• Espaço: é um conjunto de planos, onde acontece a geometria espacial. No espaço, as figuras possuem três dimensões e volume.

Outros conceitos

• Semirretas: são retas que sem fim, ou seja, têm apenas sentido e direção, sem indicação de origem;
• Segmento de retas: retas divididas em dois pontos que têm tamanhos definidos. Estas podem ser classificadas em quatro: consecutivas, colineares, adjacentes e congruentes;
• Ângulos: onde dois segmentos de retas se encontram. Possuem grau de abertura e podem ser classificados em cinco: nulo, agudo, reto, obtuso e raso.

Além dos conceitos, existem duas classificações de figuras bidimensionais dentro da geometria plana que nos ajudam a entender as fórmulas.

As classificações são:

• Polígonos: figuras fechadas e formadas por segmentos de retas;
• Não polígonos: abertos ou fechados, são formados não totalmente por segmentos de retas.

Agora que você já compreendeu qual é a diferença entre área e perímetro e como funciona a geometria plana, vamos falar sobre cada um deles e aprender como calculá-los.

🔵Leia também: Como calcular a nota do Enem: um guia prático para saber sua média

O que é área?

A área é a medida total de uma superfície, ou seja, todo o espaço que ela ocupa dentro de um plano, não apenas o seu contorno.

E para conseguir calcular a área de uma figura plana é necessário analisar a figura e saber com qual delas estamos lidando.

Algumas das figuras são:

• Triângulo: é uma figura plana formada por três segmentos de retas, tendo três lados e ângulos internos que somam 180°;
• Quadrado: um polígono que tem quatro lados iguais e quatro segmentos de retas Está presente no grupo dos quadriláteros, figuras com quatro lados. Possui ângulos internos retos (90°) e iguais;
• Retângulo: O retângulo é um paralelogramo (formas de quatro lados iguais cujos lados opostos são paralelos) que tem todos os ângulos internos retos, ou seja, com 90°.
• Trapézio: também é um paralelogramo que possui seis lados. A soma de seus ângulos internos chega a 360°;
• Losango: O losango também é um paralelogramo e um quadrilátero. Possui diagonais paralelas que formam um ângulo de 90°;
• Círculo: Já o círculo não é um paralelogramo, nem um quadrilátero e nem um polígono. O círculo é um não polígono, pois é uma figura formada apenas de pontos no plano. Ele é composto pelo raio (r), que é o valor da distância entre o centro do círculo e seu contorno.

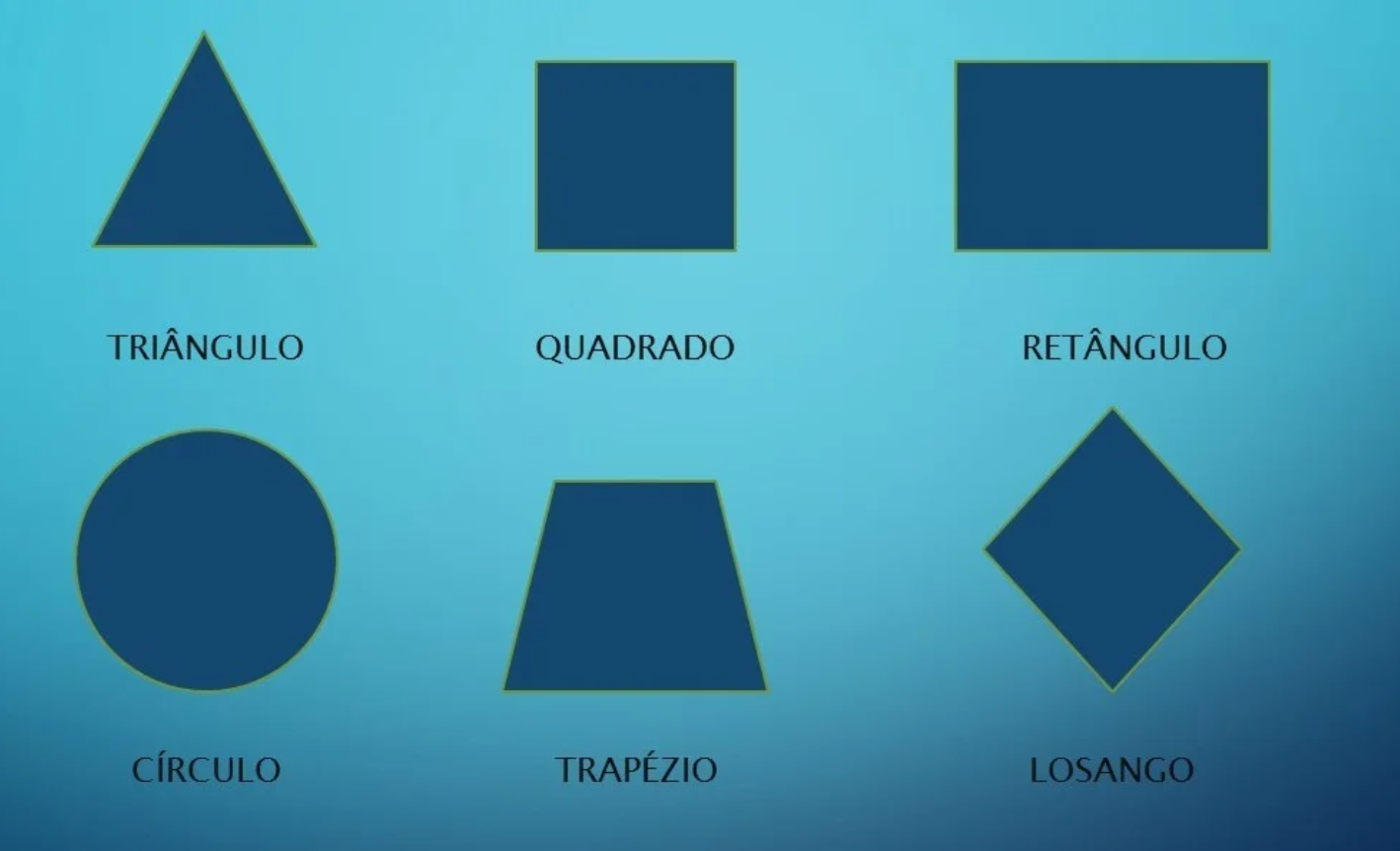
Fonte: todamateria.com.br

Sabendo quais são as figuras e suas características, fica mais fácil entender qual fórmula utilizar.

Como se calcula a área?

Cada uma das figuras planas têm uma fórmula própria que podemos utilizar para chegar nas medidas de área.

As principais são:

• Triângulo: para chegar na área do triângulo, precisamos multiplicar a base pela altura e dividir por dois usando a fórmula A = b * h / 2 (Sendo b a base e h a altura);
• Quadrado: a área do quadrado é determinada elevando ao quadrado a medida de um dos lados. A fórmula é a seguinte: A = l² (Sendo l, o lado);
• Retângulo: podemos determinar a área do retângulo multiplicando a base pela altura com a fórmula A = b * h (Sendo b a base e h, altura);
• Trapézio: a fórmula para chegar na medida de área do trapézio é A = (B + b) * h / 2, sendo a soma da base maior com a base menor multiplicada pela altura e dividida por dois. Na fórmula, B é a base maior, b é a base menor e h, a altura;
• Losango: para calcular a área de um losango, é necessário multiplicar as diagonais e dividir por dois. A fórmula é a seguinte: A = D * d / 2 (sendo D a diagonal maior e d, a menor);
• Círculo: a área do círculo é calculada utilizando o π, uma constante de valor 3,14. A fórmula é a seguinte: A = π * r² (sendo r, a medida do raio, ou seja, a medida do centro do círculo até seu contorno).

Entendido como se calcula a área, e as fórmulas usadas, vamos falar sobre o perímetro.

🔵Leia também: Pontuação do Enem: quanto precisa alcançar para entrar na faculdade?

O que é perímetro?

O perímetro, por sua vez, nada mais é do que a medida do contorno de uma figura. Medir o perímetro significa medir todos os lados de uma figura plana.

Caso seja possível, a maneira mais fácil de medir o perímetro de uma figura é passando uma fita métrica ao redor.

Porém, para facilitar esse processo, é possível medir o perímetro através de cálculos.

Como se calcula o perímetro?

O método usado para calcular o perímetro de cada figura plana varia. Por isso, vamos falar sobre os principais abaixo:

Polígonos

Os polígonos, como explicamos acima, são figuras planas fechadas e formadas totalmente por segmentos de retas.

Ou seja, os polígonos não têm curvas e seus segmentos de retas se encontram em extremidades que criam ângulos.

Para medir o perímetro de um polígono, basta somar as medidas de todos os lados.

E, para isso, existem algumas fórmulas que você pode usar:

• Triângulo: P = a + b + c (Sendo que cada letra representa um dos lados do triângulo);
• Quadrado e Losango: P = 4l (Sendo l, os lados do quadrado);
• Retângulo: P = 2b + 2h (Sendo b, a base e h, a altura);
• Trapézio: P = B + b + l1 e l2 (Sendo B a base maior, b a base menor, l₁ um dos lados e l₂, o outro).

Além disso, para calcular o perímetro de polígonos regulares, pode-se utilizar a seguinte fórmula: P = n·s (Sendo P o perímetro, n o número de lados e s, o comprimento de cada lado.

Círculo

Medir o perímetro de um círculo significa medir sua circunferência. E isso pode ser feito utilizando uma fórmula simples: C = 2πr

Ou seja, a circunferência é igual a duas vezes Pi multiplicado pelo raio.

Por isso, para descobrir o perímetro de um círculo é preciso, primeiro, descobrir a medida de seu raio.

Figuras Mistas

As figuras mistas são não polígonos, aquelas que não são formadas totalmente de segmentos de retas e nem totalmente formadas de pontos, como os círculos.

Elas são formadas por pontos e retas e nesses casos é necessário calcular as partes que a formam separadamente, como no exemplo da figura abaixo:

Fonte: mundoeducacao.uol.com.br

Sendo metade círculo e metade quadrado, precisamos calcular tanto a circunferência quanto os lados do quadrado e somar os dois resultados depois.

🔵Leia também: Como entrar na faculdade? Conheça as principais formas de ingresso

Exercícios de área e perímetro para você praticar

Agora que você já entendeu como calcular a área e perímetro de figuras planas, vamos aos exercícios para praticar. Na conclusão deste artigo, você encontra as respostas corretas.

Questão 1

[Enem 2016] Um senhor, pai de dois filhos, deseja comprar dois terrenos, com áreas de mesma medida, um para cada filho. Um dos terrenos visitados já está demarcado e, embora não tenha um formato convencional (como se observa na Figura B), agradou ao filho mais velho e, por isso, foi comprado. O filho mais novo possui um projeto arquitetônico de uma casa que quer construir, mas, para isso, precisa de um terreno na forma retangular (como mostrado na Figura A) cujo comprimento seja 7m maior do que a largura.

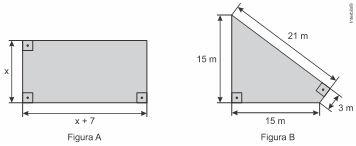
Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metros, do comprimento e da largura sejam iguais, respectivamente, a

1. 7,5 e 14,5.
2. 9,0 e 16,0.
3. 9,39,3 e 16,3.
4. 10,0 e 17,0.
5. 13,5 e 20,5.

Questão 2

[ENEM 2013] Para o reflorestamento de uma área, deve-se cercar totalmente, com tela, os lados de um terreno, exceto o lado margeado pelo rio, conforme a figura. Cada rolo de tela que será comprado para confecção da cerca contém 48 metros de comprimento.

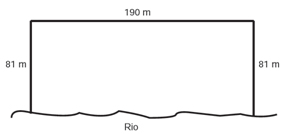
A quantidade mínima de rolos que deve ser comprada para cercar esse terreno é

1. 6.
2. 7.
3. 8.
4. 11.
5. 12.

Conclusão

Chegando ao final deste conteúdo, esperamos que você tenha conseguido entender o que é área e perímetro e que tenha aproveitado os exercícios.

Confira as respostas das questões:

• Questão 1 [Enem 2016] - Alternativa B
• Questão 2 [Enem 2013] - Alternativa C